Part 1 of this series introduced the concepts of Proportional (P), Integral (I), and Derivative (D) terms in a PID loop to automatically control a process so that it can react to unforeseen changes. The changes can be either in the Process Variable (PV) or Setpoint (SP) and it is brought under control by altering the Control Variable (CV). In this blog post we will explore the role played by each term using simplified examples and basic arithmetic.
Proportional Component
The Proportional (P) term simply multiplies the difference between where you want to be and where you are right now and passes it to the output, i.e. the Error (difference between SP and PV). A small P term means multiplying the Error by a small number which results in a feeble reaction. The choice of P determines the responsiveness of your system. Interestingly, the same P value will produce different responses in different types of processes.
Example 1
A VFD pump is used to maintain discharge pressure in a water distribution system. The discharge pressure created by the VFD is determined not only by its speed but also by the system demand. Let us use an arbitrary example where:
- desired discharge pressure (SP) is 50 psi
- measured discharge pressure (PV) is 40 psi
- PID parameters are P = 2, I = 0, and D = 0
- VFD speed command (CV) will be varied to get the PV to be equal to SP
Error in the system is:
Error = SP – PV = 50 – 40 = 10 psi
Speed of the VFD (CV) is calculated by:
CV = Error * P = 10 * 2 = 20 Hz
For a different perspective, imagine the measured pressure (PV) changes from 45 psi to 38 psi because of increased demand and the P term is set to 1. Change in VFD speed command is calculated as:
CVinitial = Error * P = (50-45) * 1 = 5 Hz
CVfinal = Error * P = (50-38) * 1 = 12 Hz
Change in CV = CVfinal - CVinitial = 12 – 5 = 7 Hz
In other words, setting the P term to 1 allows the CV to change proportional to the change in Error.
Tips and tricks
- If small changes in CV causes quick and large changes in PV then keep your P term small
- If PV overshoots and oscillates around SP then reduce your P term
- If PV reaches a steady state but is below the SP then introduce the Integral term
The dark line is the CV as a response to change and the lighter line is the SP:
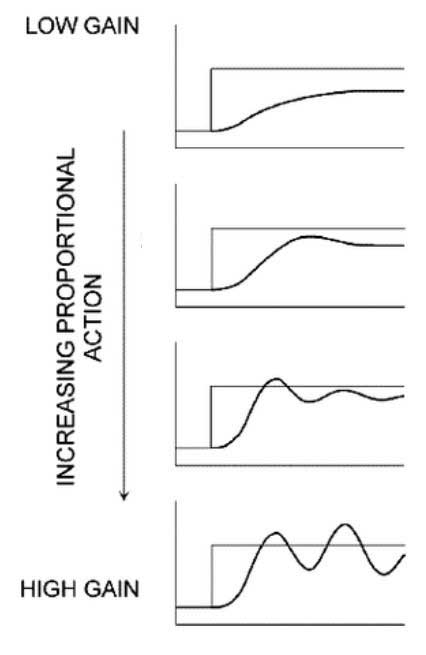
[https://www.researchgate.net/figure/Tuning-Map-for-Proportional-and-Integral-Effects-Harold-2004_fig4_319291946]
Integral Component
The Integral (I) term looks at how much Error is there and for how long. Consider the Integral term as something that makes up for what the P term could not achieve in a reasonable time. For historical reasons, the Integral term is also known as ‘Reset’. It is either mentioned as repeats per minute or its inverse. Another perspective is to view the ‘I’ term (in units of minutes per repeat) as the time it takes the output to increase by the Proportional amount.
Example 2
Using the same VFD from Example 1, let us use another arbitrary example where:
- desired discharge pressure (SP) is 50 psi
- measured discharge pressure (PV) is 40 psi
- PID parameters are P = 2, I = 1 minute, and D = 0
The Proportional output would be:
CV = Error * P = (50 - 40) * 2 = 20 Hz
Since the Integral term is set to 1 minute, the output will increase by 20 Hz in 1 minute, another 20 Hz in the next minute and so on until it reaches maximum limit.
Tips and tricks
- The bigger the Integral term (in minutes per repeat), the slower the response will be. If the Integral is in repeats per minute then the opposite is true.
- Useful when steady state is reached but it is not equal to SP
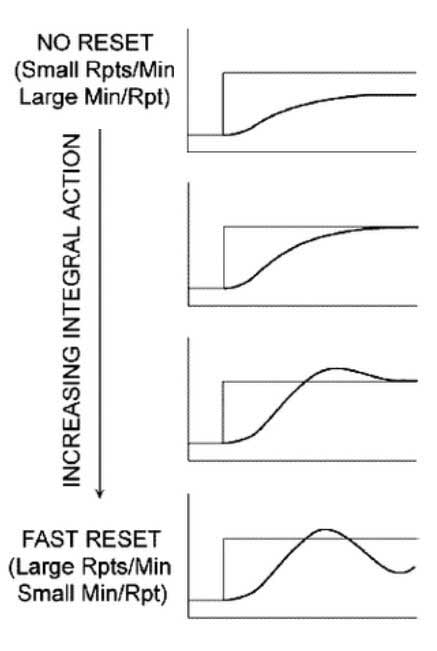
Derivative Component
The Derivative (D) term is a predictive component and it works by evaluating the rate of change of the Error. It ensures a very quick response to a change in Error, however, such rapid response can become unstable if there is noise in the process variable or a large setpoint change.
Example 3
Once again using the above VFD example:
- desired discharge pressure (SP) is 50 psi
- measured discharge pressure (PV) is 40 psi and is dropping 1 psi per minute
- PID parameters are P = 0, I = 0, and D = 10 minute/repeat
The Derivative output would be:
CV = rate of change of Error * D = (1 psi/1 minute) * 10 = 10 Hz
Thus a 1 psi drop per minute will elicit a 10 Hz change in the VFD speed.
Tuning Tips and Tricks
The above examples are a simplified static scenario presented in the interest of clarity. In practice, the situation will be dynamic where the calculated parameters will be changing continuously. Also, there are many more features of a PID control, ex. integral windup, cascade control etc, which are beyond the scope of this blog post.
As a novice, follow these steps to tune your first PID loop (as long as it is safe to do so!):
- See if you can find the PID values for a similar process and use it as a starting point, if not ……..
- Start with a small P and no I or D
- Change the SP and observe the PV
- If PV reaches a steady state way below the SP then slowly increase P until you get close to SP but not too much, otherwise PV will start oscillating
- Start adding small amounts of ‘I’ to increase the speed with which PV reaches SP and stays there
- Most systems should not need a D term but if you need it then please get in touch with a professional 😊
Is your control system getting a little long in the tooth? Check out this white paper detailing five steps you can take to make the transition efficiently and with minimal risk.



COMMENTS